Monday, April 19, 2010

Conductance

Writing

\big. U = \frac{k}{\Delta x}, \quad

where U is the conductance, in W/(m2 K).

Fourier's law can also be stated as:

\big. \frac{\Delta Q}{\Delta t} = U A\, (-\Delta T).

The reciprocal of conductance is resistance, R, given by:

\big. R = \frac{1}{U} = \frac{\Delta x}{k} = \frac{A\, (-\Delta T)}{\frac{\Delta Q}{\Delta t}}, \quad

and it is resistance which is additive when several conducting layers lie between the hot and cool regions, because A and Q are the same for all layers. In a multilayer partition, the total conductance is related to the conductance of its layers by:

\big. \frac{1}{U} = \frac{1}{U_1} + \frac{1}{U_2} + \frac{1}{U_3}+ \cdots

So, when dealing with a multilayer partition, the following formula is usually used:

\big. \frac{\Delta Q}{\Delta t} = \frac{A\,(-\Delta T)}{\frac{\Delta x_1}{k_1} + \frac{\Delta x_2}{k_2} + \frac{\Delta x_3}{k_3}+ \cdots}.

When heat is being conducted from one fluid to another through a barrier, it is sometimes important to consider the conductance of the thin film of fluid which remains stationary next to the barrier. This thin film of fluid is difficult to quantify, its characteristics depending upon complex conditions of turbulence and viscosity, but when dealing with thin high-conductance barriers it can sometimes be quite significant.

Intensive-property representation

The previous conductance equations written in terms of extensive properties, can be reformulated in terms of intensive properties.

Ideally, the formulae for conductance should produce a quantity with dimensions independent of distance, like Ohm's Law for electrical resistance: R = V/I\,\!, and conductance: G = I/V \,\!.

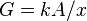From the electrical formula: R = \rho x / A \,\!, where ρ is resistivity, x = length, A cross sectional area, we have G = k A / x \,\!, where G is conductance, k is conductivity, x = length, A = cross sectional area.

For Heat,

\big. U = \frac{k A} {\Delta x}, \quad

where U is the conductance.

Fourier's law can also be stated as:

\big. Q = U \, \Delta T \quad

analogous to Ohm's law: I = V/R \,\! or I = V G. \,\!

The reciprocal of conductance is resistance, R, given by:

\big. R = \frac{\, \Delta T}{Q}, \quad

analogous to Ohm's law: R = V/I. \,\!

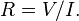
The sum of conductances in series is still correct.

Cylinders

Conduction through cylinders can be calculated when variables such as the internal radius r1, the external radius r2, and the length denoted as 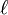\ell.

The temperature difference between the inner and outer wall can be expressed as T2 − T1.

The area of the heat flow: 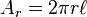A_r= 2 \pi r \ell

When Fourier’s equation is applied:

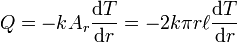
Q = -k A_r \frac{\mathrm{d}T}{\mathrm{d}r} = -2 k \pi r \ell \frac{\mathrm{d}T}{\mathrm{d}r}

Rearranged:

Q \int_{r_1}^{r_2} \frac{1}{r} \mathrm{d}r = -2 k \pi \ell \int_{r_1}^{r_2} \mathrm{d}T

Therefore the rate of heat transfer is

Q = 2 k \pi \ell \frac{T_1 - T_2}{\ln r_2 - \ln r_1}

The thermal resistance is

R_c = \frac{\Delta T}{Q} = \frac{\ln r_2 - \ln r_1}{2 \pi k \ell}

And Q = 2 \pi k \ell r_m \frac{T_1-T_2}{r_2-r_1}, where r_m = \frac{r_2-r_1}{\ln r_2 - \ln r_1} and it is important to note that this is the log-mean radius.

Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)