The law of Heat Conduction, also known as Fourier's law, states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area at right angles, to that gradient, through which the heat is flowing. We can state this law in two equivalent forms: the integral form, in which we look at the amount of energy flowing into or out of a body as a whole, and the differential form, in which we look at the flows or fluxes of energy locally.
Differential form
The differential form of Fourier's Law of thermal conduction shows that the local heat flux,  , is equal to the product of thermal conductivity, k, and the negative local temperature gradient,
, is equal to the product of thermal conductivity, k, and the negative local temperature gradient,  . The heat flux is the amount of energy that flows through a particular surface per unit area per unit time.
. The heat flux is the amount of energy that flows through a particular surface per unit area per unit time.
where (including the SI units)
 is the local heat flux, [W·m−2]
is the local heat flux, [W·m−2] is the material's conductivity, [W·m−1·K−1],
is the material's conductivity, [W·m−1·K−1], is the temperature gradient, [K·m−1].
is the temperature gradient, [K·m−1].
The thermal conductivity, k, is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case k is represented by a second-order tensor. In nonuniform materials, k varies with spatial location.
For many simple applications, Fourier's law is used in its one-dimensional form. In the x-direction,
Integral form
By integrating the differential form over the material's total surface S, we arrive at the integral form of Fourier's law:
where (including the SI units)
 is the amount of heat transferred per unit time [W] and
is the amount of heat transferred per unit time [W] and is an oriented surface area element [m2]
is an oriented surface area element [m2]
The above differential equation, when integrated for a homogeneous material of 1-D geometry between two endpoints at constant temperature, gives the heat flow rate as:
where
- A is the cross-sectional surface area,
- ΔT is the temperature difference between the ends,
- Δx is the distance between the ends.
This law forms the basis for the derivation of the heat equation. Ohm's law is the electrical analogue of Fourier's law.


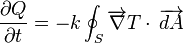

nice blog !! thanks for sharing the information about conduction and about fourier's law
ReplyDelete